Two-Way Crossover Network Design | ||
The first and most important concept for you to understand before you design any passive crossover is that all the formulas are derived with the assumption that you are terminating into a constant impedance load. This means that the values these formulas give are only correct for the impedance value you input into the formula. This is great if you are using a speaker with ferro-fluid (a magnetic fluid in the voice-coil gap which modifies the impedance to a relatively flat value), however, in general a speaker's impedance varies greatly over the operating range of the driver. So before you calculate a passive crossover network, you must first correct the inherent impedance problems common in dynamic loudspeakers. | ||
The first problem is the impedance peak present at the resonant frequency of the speaker. The exact frequency and shape of this peak is variable depending on the type of enclosure loading you are using with the driver. The graphic below will illustrate this point clearly. | ||
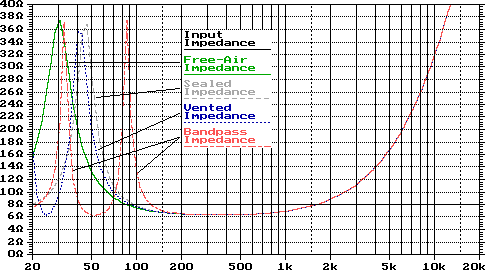 | ||
As you can see, using the manufacturer's rated impedance is not a good idea. However, you can correct this impedance peak so the formulas are useful again. I would also like you to notice the impedance curving upwards in the higher frequency range. This is caused by the inductance of the voice-coil. This too can be corrected. | ||
The first problem we will address is the peak at resonance. This can be fixed using a contour network. This filter type is covered here. | ||
To correct the rising impedance in the higher frequencies, you need to utilize a different type of impedance shaping filter. | ||
| Explanation of Terms Used in the Formulas | ||
| C1, C2, C3, etc... are the capacitor values required for your crossover network. | ||
| L1, L2, L3, etc... are the inductor values required for your crossover network. | ||
| Rh is the impedance of the speaker at the frequency you want to apply your high pass filter. | ||
| RL is the impedance of the speaker at the frequency you want to apply your low pass filter. | ||
| f is the frequency which you are calculating the crossover for. | ||
| A bandpass filter can be used to limit how high or low the frequency range being sent to a speaker is. This can be useful when limited excursion drivers are used for the bass range in a two-way speaker system. | ||
| Links to the Calculators/Diagrams/Formulas | |||
| 1st Order Butterworth | |||
| 2nd Order Butterworth | 2nd Order Linkwitz-Riley | ||
| 3rd Order Butterworth | |||
| 4th Order Butterworth | 4th Order Linkwitz-Riley | ||
| 6th Order Linkwitz-Riley | |||
Next Accessories Home Links Loudspeakers 101 Software E-Mail